How To Graph A Solution Set Of Inequalities

Solutions to Inequalities with 2 Variables

We know that a linear equation with 2 variables has infinitely many ordered pair solutions that form a line when graphed. A linear inequality with ii variablesAn inequality relating linear expressions with two variables. The solution set is a region defining half of the airplane. , on the other hand, has a solution set consisting of a region that defines half of the plane.

Linear Equation	Linear Inequality
$y=\frac{3}{2}x+3$	$y\le \frac{\mathrm{iii}}{2}x+\mathrm{three}$

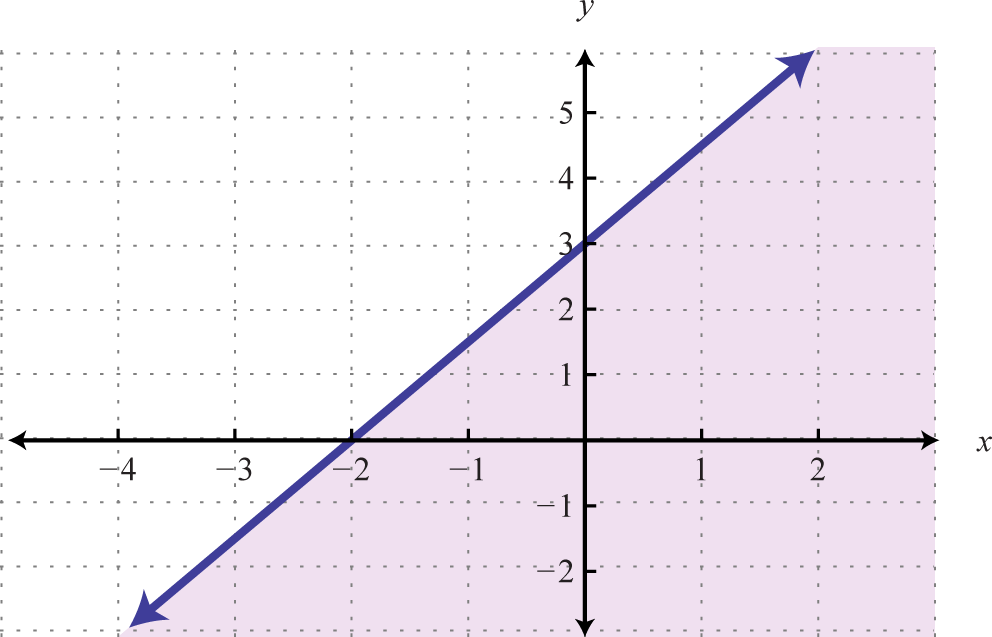
For the inequality, the line defines the boundary of the region that is shaded. This indicates that any ordered pair in the shaded region, including the boundary line, will satisfy the inequality. To run across that this is the instance, cull a few exam pointsA betoken not on the purlieus of the linear inequality used as a means to determine in which half-plane the solutions lie. and substitute them into the inequality.

Exam bespeak	$y\le \frac{3}{\mathrm{ii}}x+3$
(0, 0)	$\begin{array}{l}0\le \frac{3}{2}\left(0\right)+\mathrm{iii}\\ 0\le 3\text{✓}\end{array}$
(2, i)	$\begin{array}{l}\mathrm{ane}\le \frac{\mathrm{three}}{2}\left(2\right)+\mathrm{iii}\\ \mathrm{ane}\le 3+3\\ \mathrm{ane}\le \mathrm{half-dozen}\text{✓}\end{array}$
(−ii, −one)	$\begin{array}{l}-1\le \frac{\mathrm{iii}}{\mathrm{two}}\left(-2\right)+3\\ -1\le -3+\mathrm{iii}\\ -1\le 0\text{✓}\end{array}$

Also, we can meet that ordered pairs outside the shaded region practice not solve the linear inequality.

Test bespeak	$y\le \frac{\mathrm{iii}}{2}x+\mathrm{three}$
(−2, iii)	$\begin{array}{l}\mathrm{three}\le \frac{\mathrm{iii}}{\mathrm{ii}}\left(-2\right)+\mathrm{three}\\ 3\le -3+3\\ \mathrm{three}\le 0\text{✗}\end{array}$

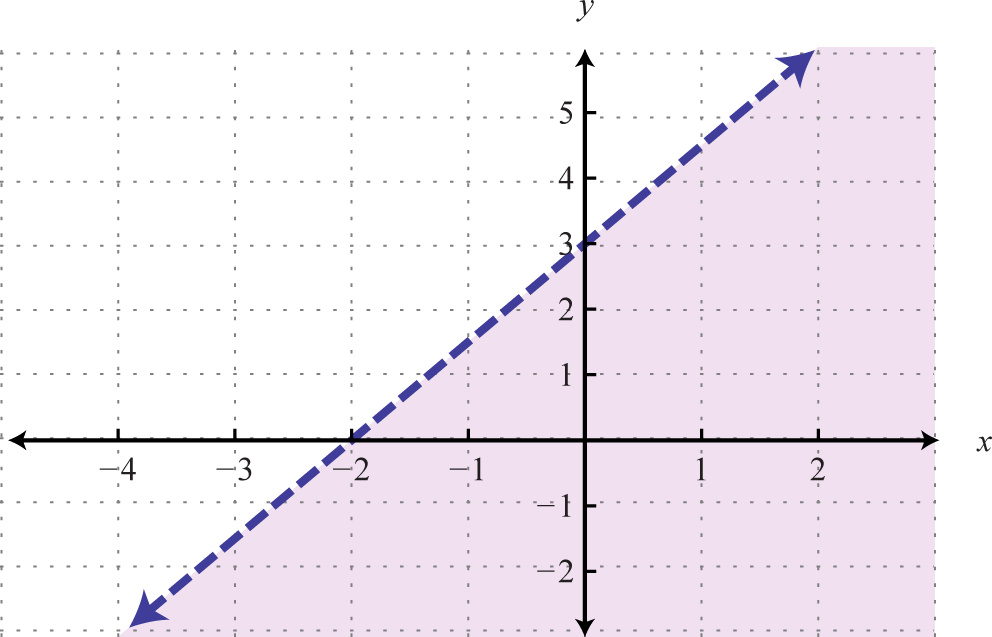
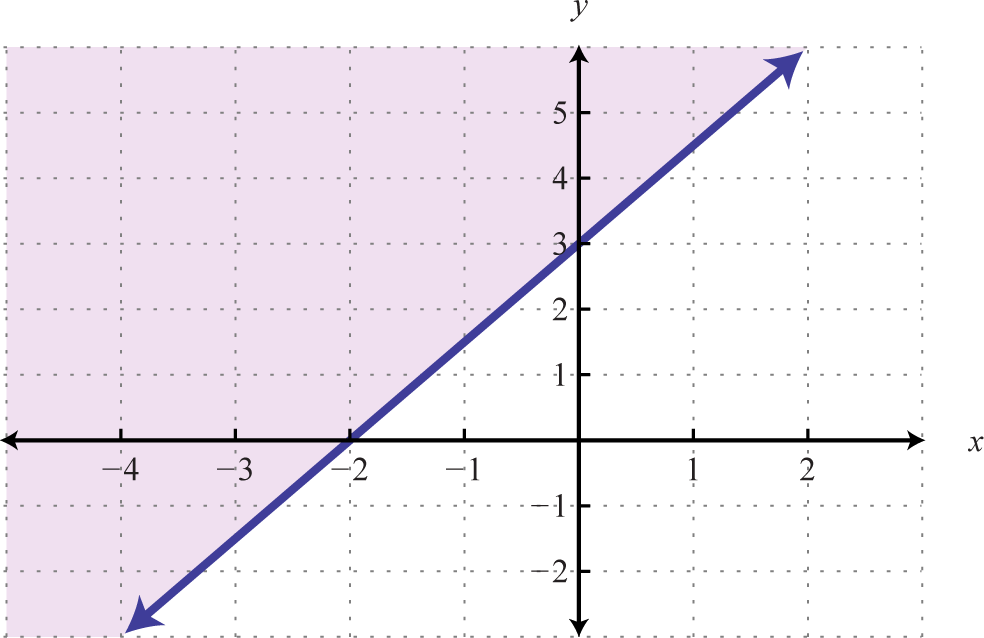
The graph of the solution set to a linear inequality is always a region. Still, the boundary may not ever be included in that set. In the previous example, the line was part of the solution set because of the "or equal to" function of the inclusive inequality $\le .$ If given a strict inequality $<$ , we would then use a dashed line to indicate that those points are non included in the solution set up.

Non-Inclusive Boundary	Inclusive Boundary
$y<\frac{3}{2}x+3$	$y\le \frac{\mathrm{three}}{2}x+3$

Consider the point (0, 3) on the boundary; this ordered pair satisfies the linear equation. It is the "or equal to" part of the inclusive inequality that makes the ordered pair part of the solution set.

$y<\frac{\mathrm{three}}{\mathrm{ii}}\mathrm{10}+3$	$y\le \frac{3}{\mathrm{two}}x+3$
$\begin{array}{l}3<\frac{\mathrm{three}}{\mathrm{ii}}\left(0\right)+3\\ 3<0+\mathrm{three}\\ 3<\mathrm{iii}\text{✗}\end{array}$	$\begin{array}{l}3\le \frac{3}{2}\left(0\right)+\mathrm{iii}\\ 3\le 0+3\\ \mathrm{three}\le 3\text{✓}\end{array}$

And so far we take seen examples of inequalities that were "less than." Now consider the post-obit graphs with the same boundary:

Greater Than (Above)	Less Than (Beneath)
$y\ge \frac{\mathrm{three}}{2}\mathrm{10}+\mathrm{iii}$	$y\le \frac{3}{\mathrm{ii}}\mathrm{10}+\mathrm{three}$

Given the graphs to a higher place, what might we expect if we use the origin (0, 0) as a test point?

$y\ge \frac{3}{2}x+3$	$y\le \frac{3}{2}\mathrm{10}+3$
$\begin{array}{l}0\ge \frac{3}{\mathrm{two}}\left(0\right)+\mathrm{iii}\\ 0\ge 0+3\\ 0\ge \mathrm{three}\text{✗}\end{array}$	$\begin{array}{l}0\le \frac{3}{\mathrm{two}}\left(0\right)+3\\ 0\le 0+3\\ 0\le 3\text{✓}\end{array}$

Example one

Make up one's mind whether or not $\left(2,\frac{\mathrm{ane}}{\mathrm{two}}\right)$ is a solution to $\mathrm{five}\mathrm{ten}-2y<10.$

Solution:

Substitute the x- and y-values into the equation and come across if a true statement is obtained.

$$\begin{array}{ccc}\hfill 5x-2y& <& 10\hfill \\ \hfill \mathrm{v}\left(\mathrm{two}\right)-2\left(\frac{1}{2}\right)& <& 10\hfill \\ \hfill 10-1& <& 10\hfill \\ \hfill 9& <& 10\text{✓}\hfill \end{array}$$

Reply: $\left(2,\frac{1}{2}\right)$ is a solution.

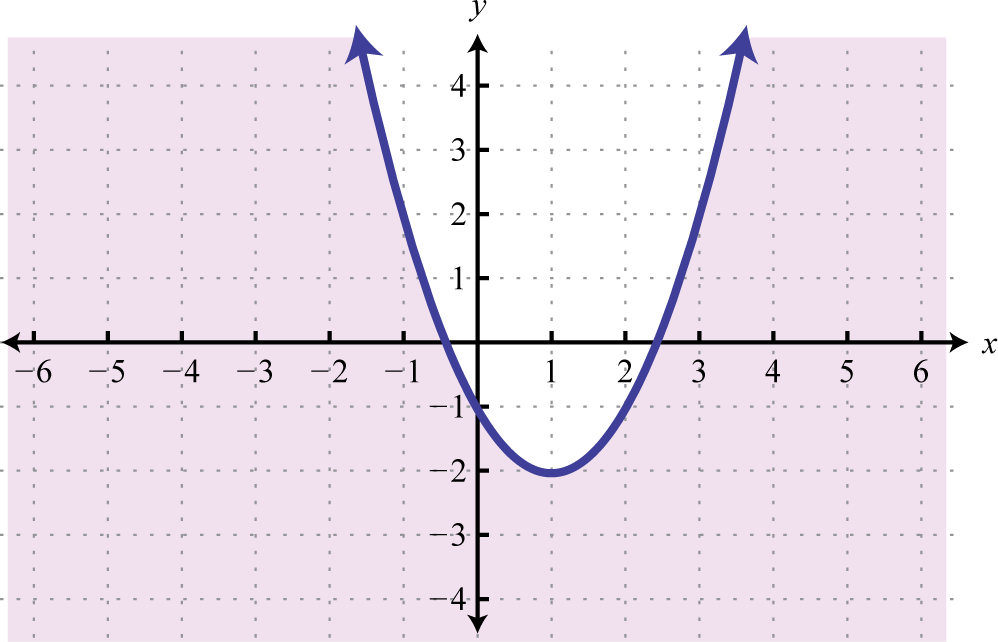
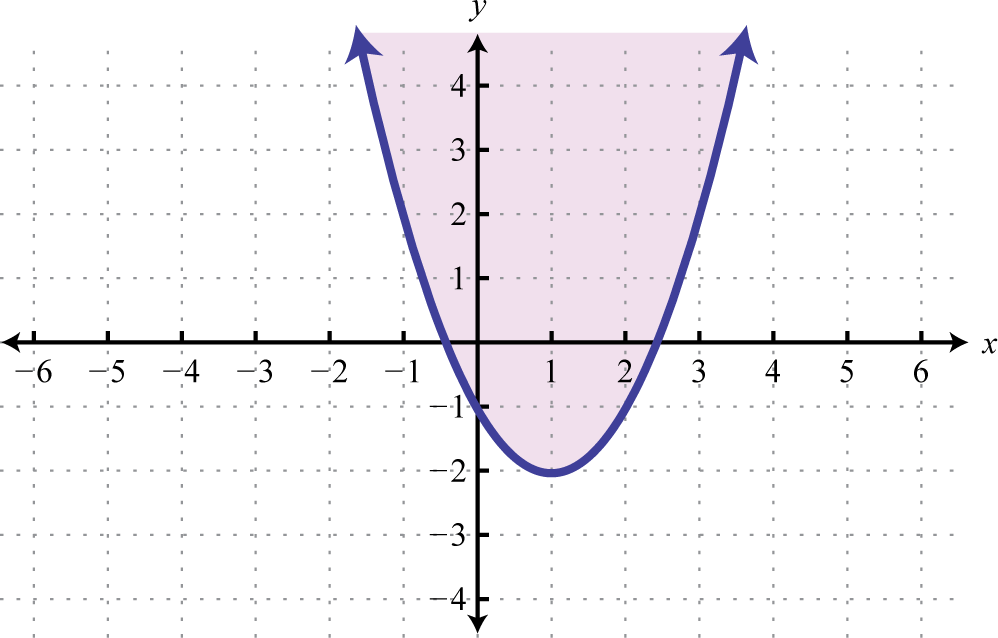
These ideas and techniques extend to nonlinear inequalities with ii variables. For example, all of the solutions to $y>x^2$ are shaded in the graph below.

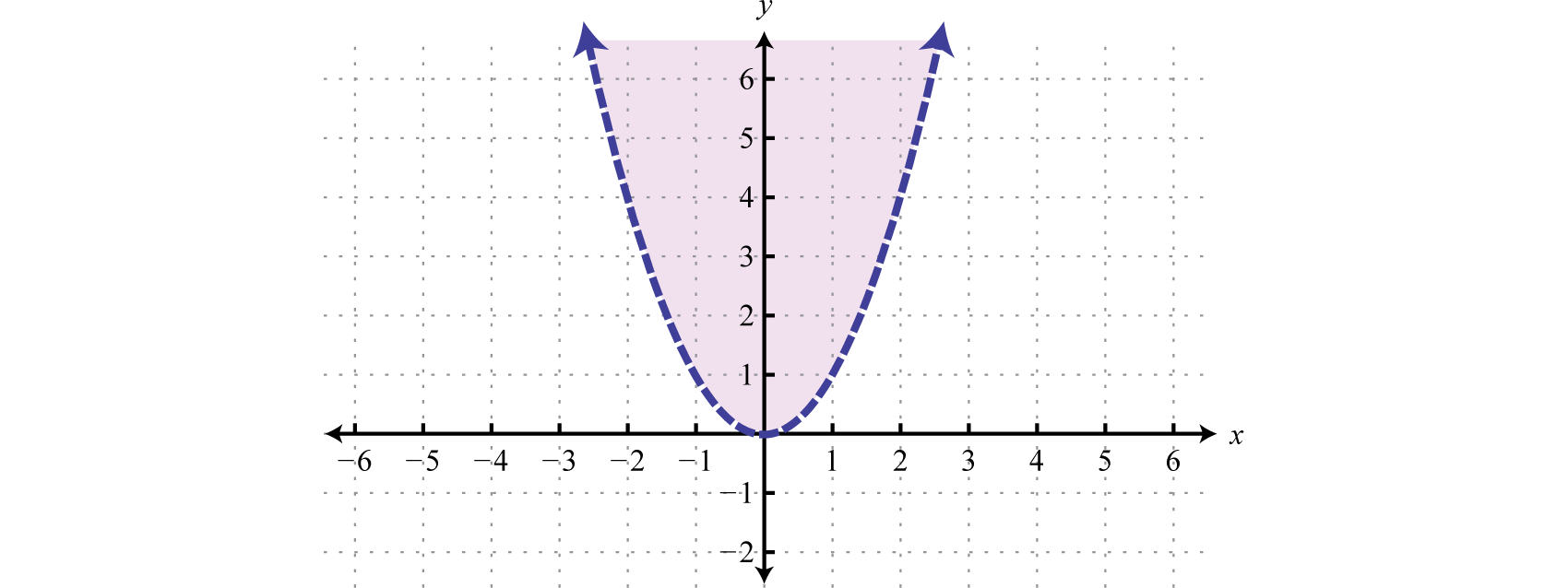
The boundary of the region is a parabola, shown as a dashed curve on the graph, and is not function of the solution set. However, from the graph we await the ordered pair (−1,4) to be a solution. Furthermore, we await that ordered pairs that are not in the shaded region, such as (−3, two), will not satisfy the inequality.

Cheque (−1,four)	Cheque (−3, 2)
$\begin{array}{l}y>x^2\\ 4>{\left(-\mathrm{ane}\right)}^2\\ 4>1\text{✓}\end{array}$	$\begin{array}{l}y>x^2\\ 2>{\left(-3\right)}^2\\ \mathrm{two}>9\text{✗}\end{array}$

Following are graphs of solutions sets of inequalities with inclusive parabolic boundaries.

$y\le {\left(\mathrm{ten}-1\right)}^2-\mathrm{two}$	$y\ge {\left(\mathrm{ten}-1\right)}^2-2$

You are encouraged to test points in and out of each solution set that is graphed to a higher place.

Attempt this! Is $\left(-3,-\mathrm{ii}\right)$ a solution to $2x-3y<0$ ?

Answer: No

Graphing Solutions to Inequalities with Ii Variables

Solutions to linear inequalities are a shaded one-half-aeroplane, bounded by a solid line or a dashed line. This purlieus is either included in the solution or not, depending on the given inequality. If nosotros are given a strict inequality, we use a dashed line to indicate that the boundary is non included. If we are given an inclusive inequality, we use a solid line to indicate that information technology is included. The steps for graphing the solution prepare for an inequality with 2 variables are shown in the following example.

Example 2

Graph the solution ready $y>-3x+\mathrm{one}.$

Solution:

• Step ane: Graph the boundary. Because of the strict inequality, we will graph the boundary $y=-3\mathrm{ten}+1$ using a dashed line. We tin can see that the slope is $\mathrm{thousand}=-\mathrm{three}=\frac{-\mathrm{three}}{1}=\frac{rise}{ru\mathrm{northward}}$ and the y-intercept is (0, 1).

  

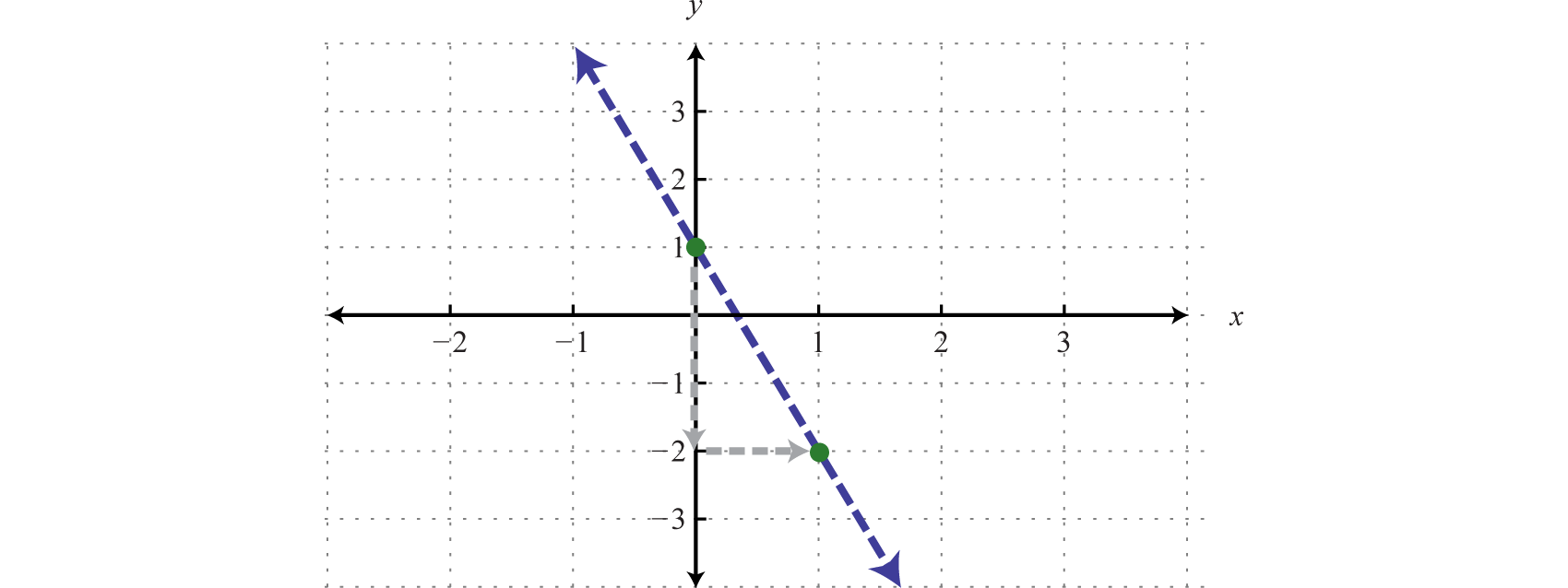
• Step 2: Test a point that is not on the boundary. A common test bespeak is the origin, (0, 0). The test indicate helps us determine which one-half of the aeroplane to shade.

  Test point	$y>-3\mathrm{ten}+1$
  (0, 0)	$\begin{array}{l}0>-3(0)+1\\ 0>1\text{✗}\end{array}$

• Footstep 3: Shade the region containing the solutions. Since the test point (0, 0) was not a solution, it does not lie in the region containing all the ordered pair solutions. Therefore, shade the half of the plane that does not contain this test indicate. In this instance, shade above the boundary line.

Reply:

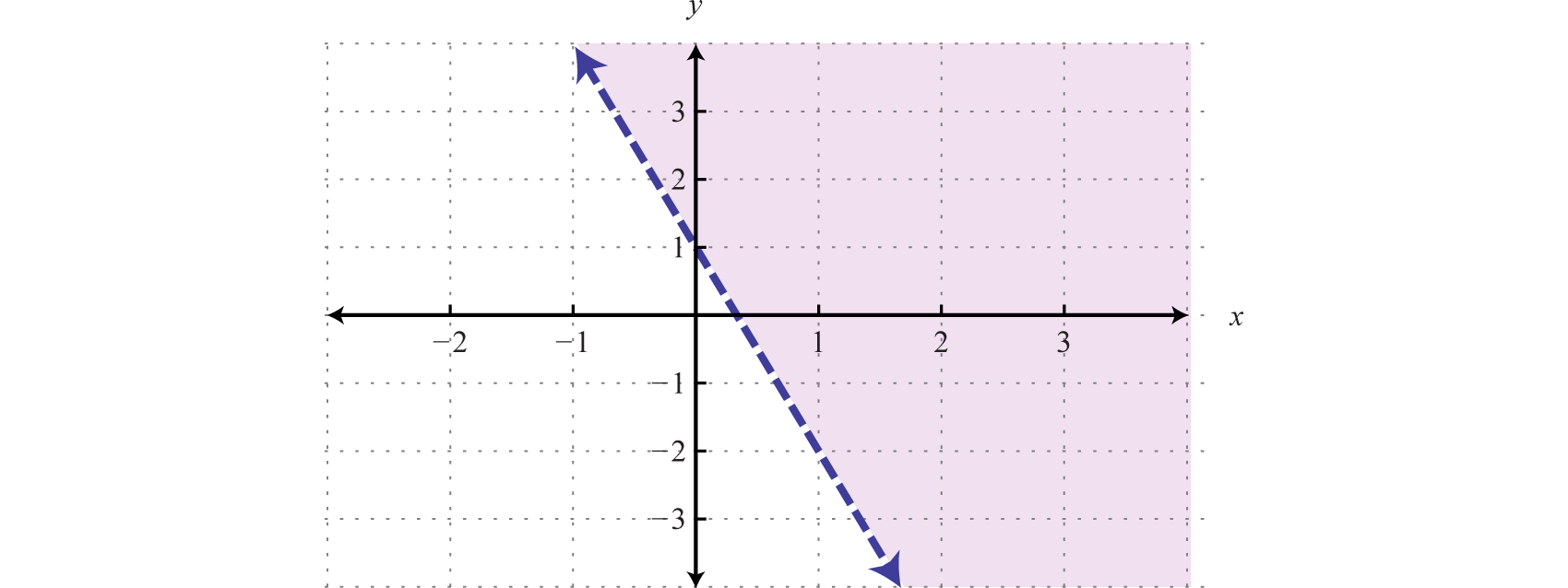
Consider the problem of shading above or beneath the boundary line when the inequality is in slope-intercept form. If $y>mx+b$ , and so shade above the line. If $y<\mathrm{yard}\mathrm{10}+b$ , then shade below the line. Shade with caution; sometimes the boundary is given in standard course, in which instance these rules do not apply.

Example 3

Graph the solution fix $\mathrm{ii}x-\mathrm{v}y\ge -10.$

Solution:

Hither the boundary is defined by the line $2\mathrm{10}-5y=-10.$ Since the inequality is inclusive, we graph the boundary using a solid line. In this example, graph the boundary line using intercepts.

To discover the x-intercept, set y = 0.	To find the y-intercept, set ten = 0.
$2x-5y=-\mathrm{ten}$ $\begin{array}{ccc}\hfill 2x-\mathrm{v}\left(0\right)& =& -10\hfill \\ \hfill 2\mathrm{ten}& =& -10\hfill \\ \hfill \mathrm{ten}& =& -5\hfill \end{array}$	$\mathrm{ii}x-5y=-10$ $\begin{array}{ccc}\hfill 2\left(0\right)-\mathrm{five}y& =& -10\hfill \\ \hfill -\mathrm{v}y& =& -\mathrm{x}\hfill \\ \hfill y& =& 2\hfill \end{array}$
ten-intercept: (−5, 0)	y-intercept: (0, 2)

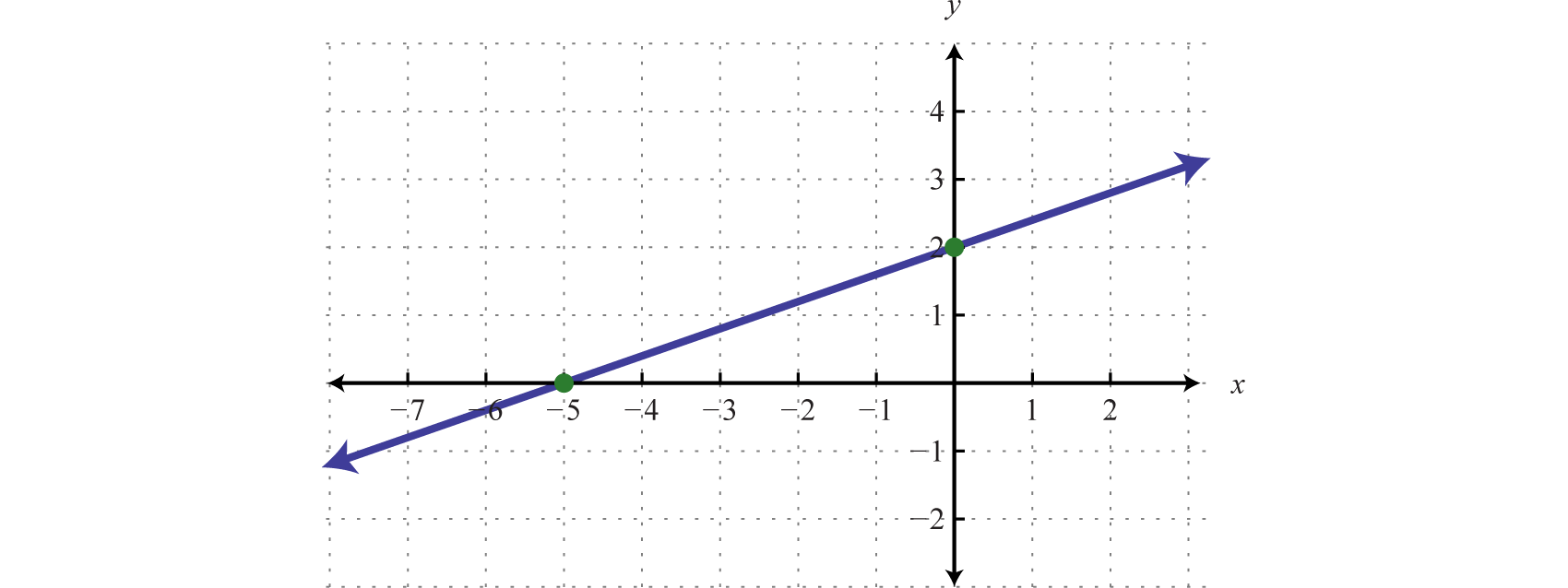
Next, test a betoken; this helps decide which region to shade.

Examination point	$2x-5y\ge -\mathrm{x}$
(0, 0)	$\begin{array}{ccc}\hfill 2\left(0\right)-\mathrm{v}\left(0\right)& \ge & -10\hfill \\ \hfill 0& \ge & -10\text{✓}\hfill \end{array}$

Since the test point is in the solution set, shade the half of the airplane that contains it.

Answer:

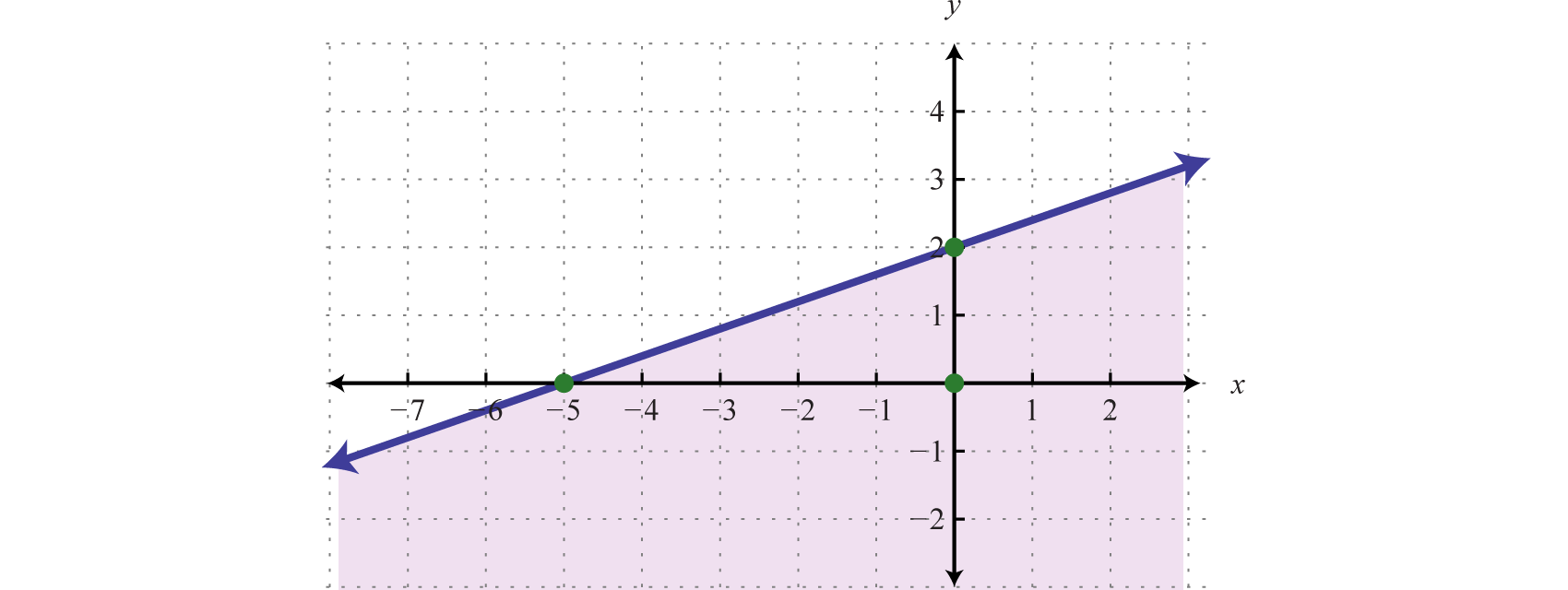
In this example, detect that the solution gear up consists of all the ordered pairs below the boundary line. This may seem counterintuitive because the original inequality involved "greater than" $\ge .$ This illustrates that information technology is a best practice to actually test a point. Solve for y and you see that the shading is correct.

$$\begin{array}{ccc}\hfill \mathrm{ii}x-\mathrm{five}y& \ge & -10\hfill \\ \hfill 2x-5y-2\mathrm{10}& \ge & -10-2\mathrm{10}\hfill \\ \hfill -\mathrm{v}y& \ge & -2x-10\hfill \\ \hfill \frac{-5y}{-5}& \le & \frac{-2x-\mathrm{x}}{-5}Rev\mathrm{east}rs\mathrm{eastward}thei\mathrm{due\; north}equality.\hfill \\ \hfill y& \le & \frac{2}{\mathrm{five}}x+\mathrm{two}\hfill \end{array}$$

In slope-intercept form, y'all tin see that the region beneath the purlieus line should be shaded. An alternate approach is to offset express the purlieus in slope-intercept course, graph information technology, and and then shade the appropriate region.

Example 4

Graph the solution fix $y<2.$

Solution:

Commencement, graph the boundary line $y=2$ with a dashed line because of the strict inequality. Side by side, test a point.

Exam point	$y<\mathrm{ii}$
(0, 0)	$0<2\text{✓}$

In this instance, shade the region that contains the test bespeak.

Reply:

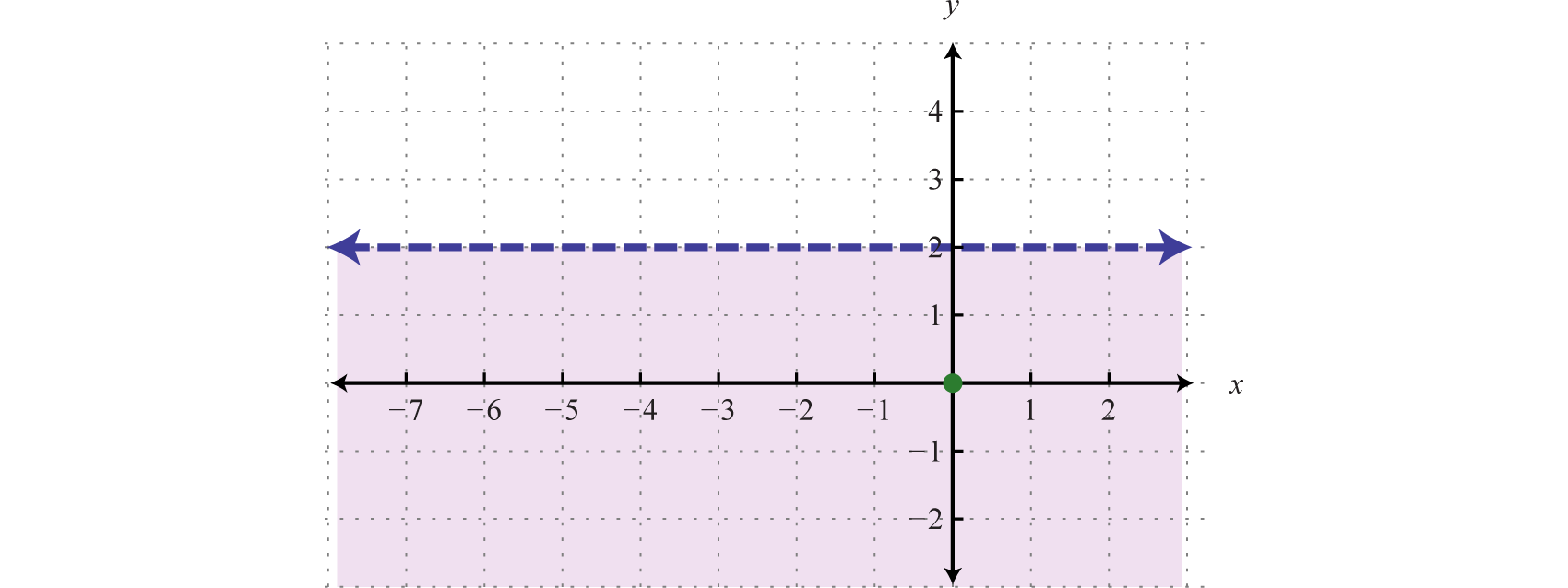
Try this! Graph the solution set $\mathrm{ii}\mathrm{10}-3y<0.$

Answer:

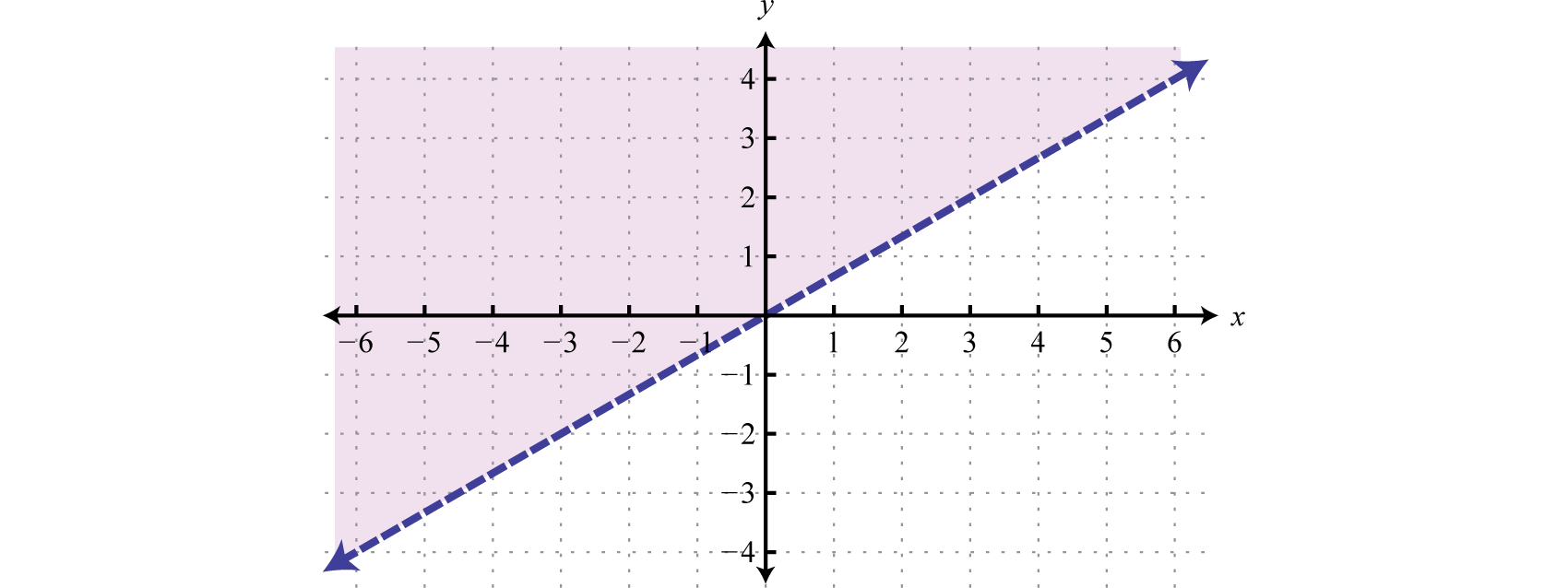
The steps are the same for nonlinear inequalities with ii variables. Graph the boundary starting time and and then test a point to determine which region contains the solutions.

Example v

Graph the solution set $y<{\left(\mathrm{ten}+\mathrm{ii}\right)}^2-1.$

Solution:

The boundary is a bones parabola shifted ii units to the left and 1 unit down. Brainstorm past drawing a dashed parabolic purlieus because of the strict inequality.

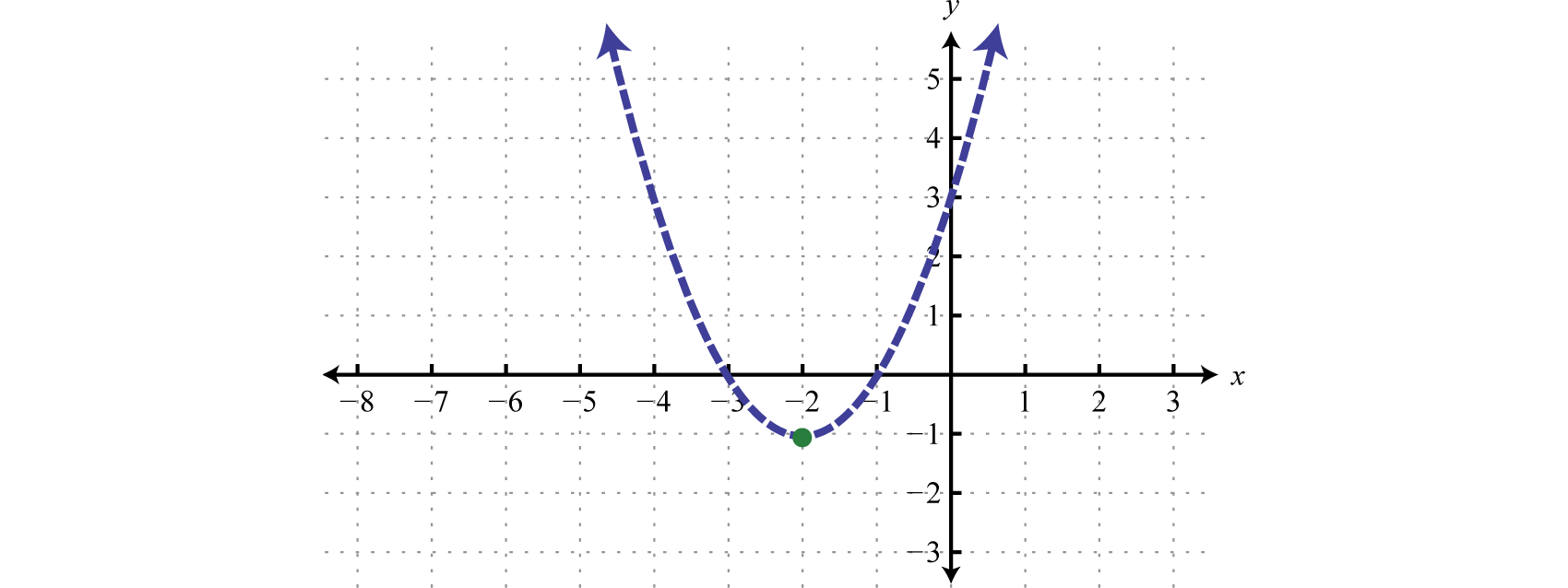
Next, test a point.

Test point	$y<{\left(x+2\right)}^{\mathrm{two}}-\mathrm{i}$
(0, 0)	$\begin{array}{l}0<{\left(0+\mathrm{ii}\right)}^2-\mathrm{ane}\\ 0<4-1\\ 0<3\text{✓}\end{array}$

In this example, shade the region that contains the exam betoken $\left(0,0\right).$

Answer:

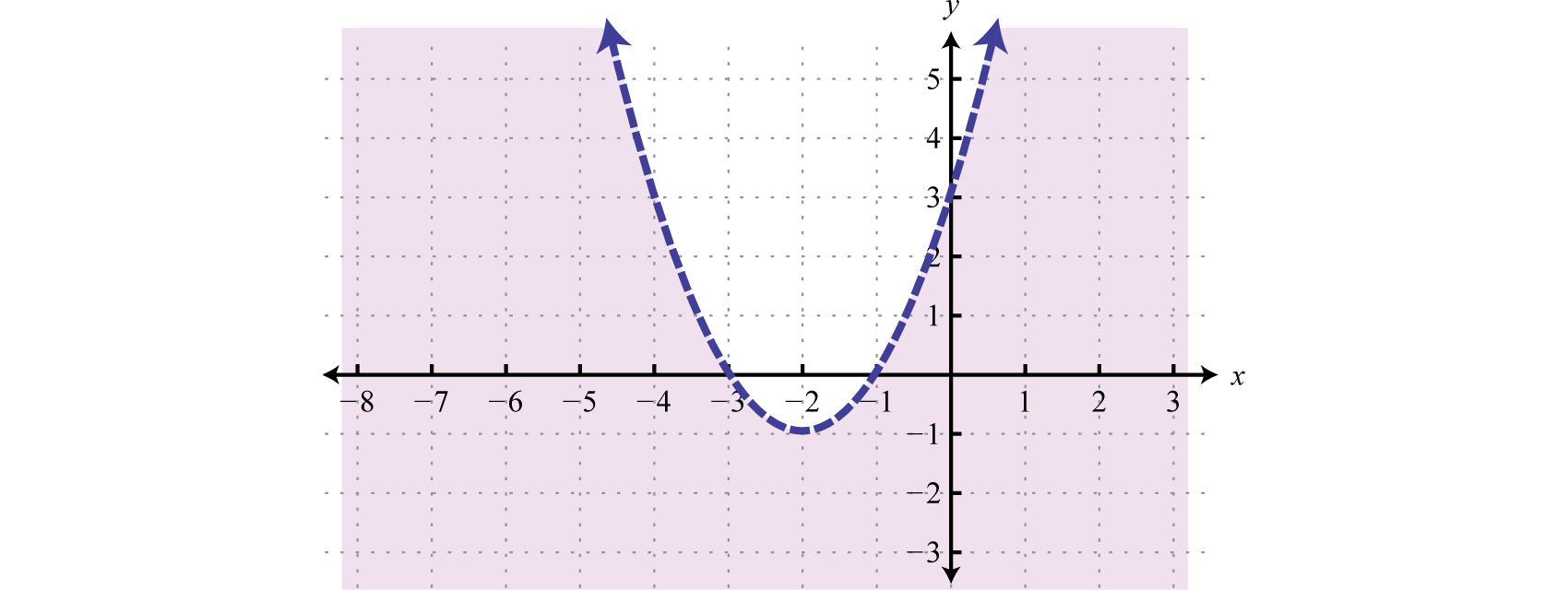
Instance 6

Graph the solution set $y\ge {\mathrm{10}}^2+3.$

Solution:

The purlieus is a basic parabola shifted 3 units up. It is graphed using a solid curve because of the inclusive inequality.

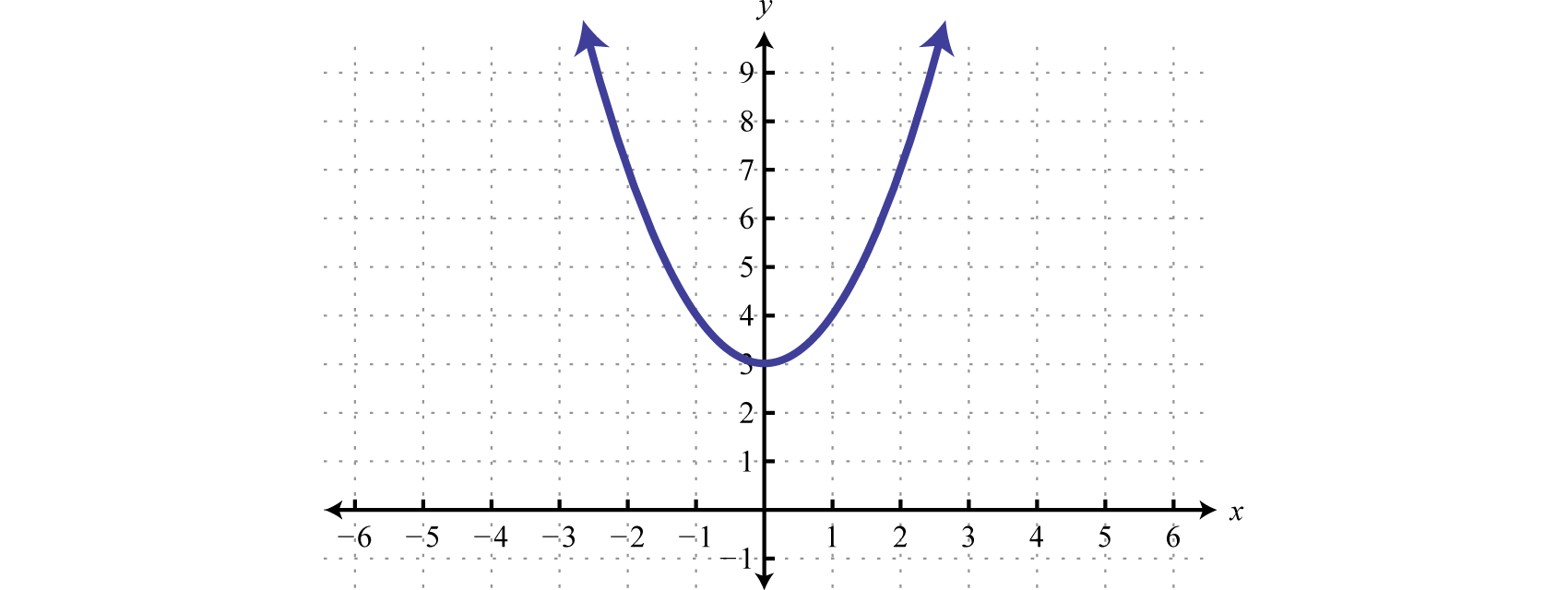
Adjacent, exam a bespeak.

Examination bespeak	$y\ge x^{\mathrm{ii}}+3$
(0, 0)	$\begin{array}{l}0\ge 0^{\mathrm{two}}+\mathrm{iii}\\ 0\ge 3\text{✗}\end{array}$

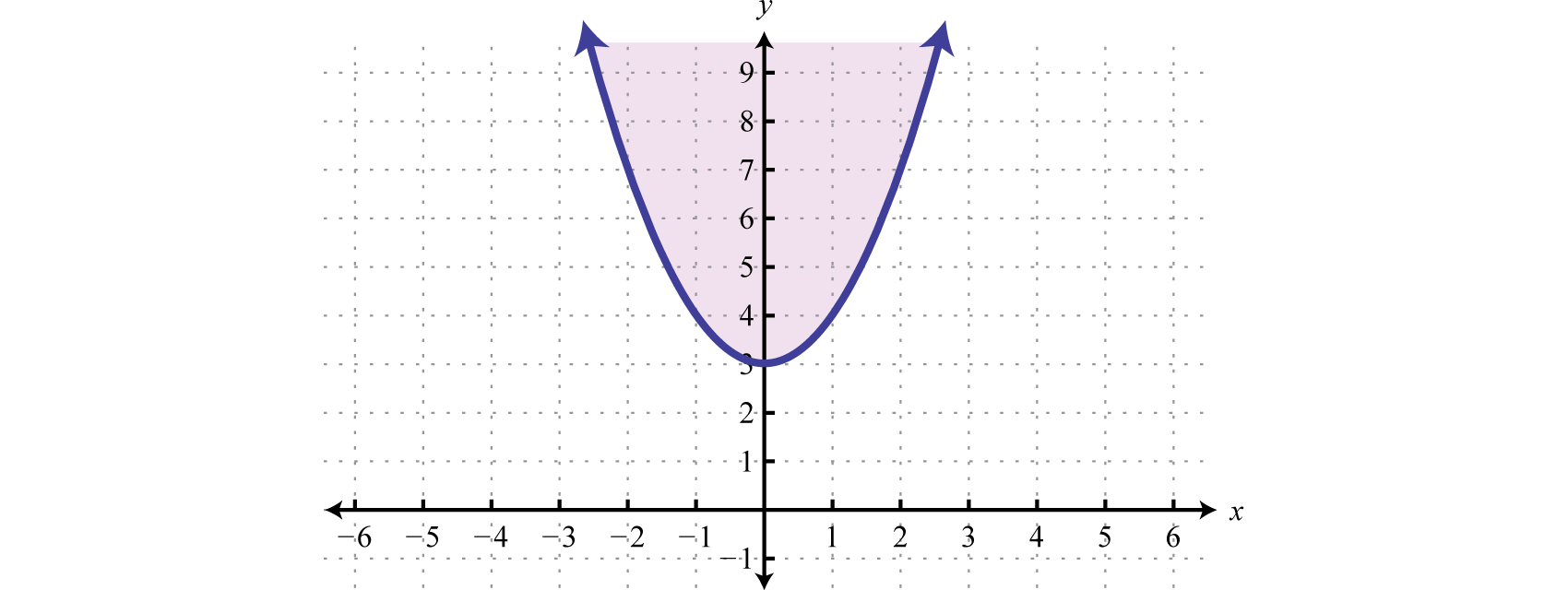
In this case, shade the region that does not contain the exam betoken $\left(0,0\right).$

Answer:

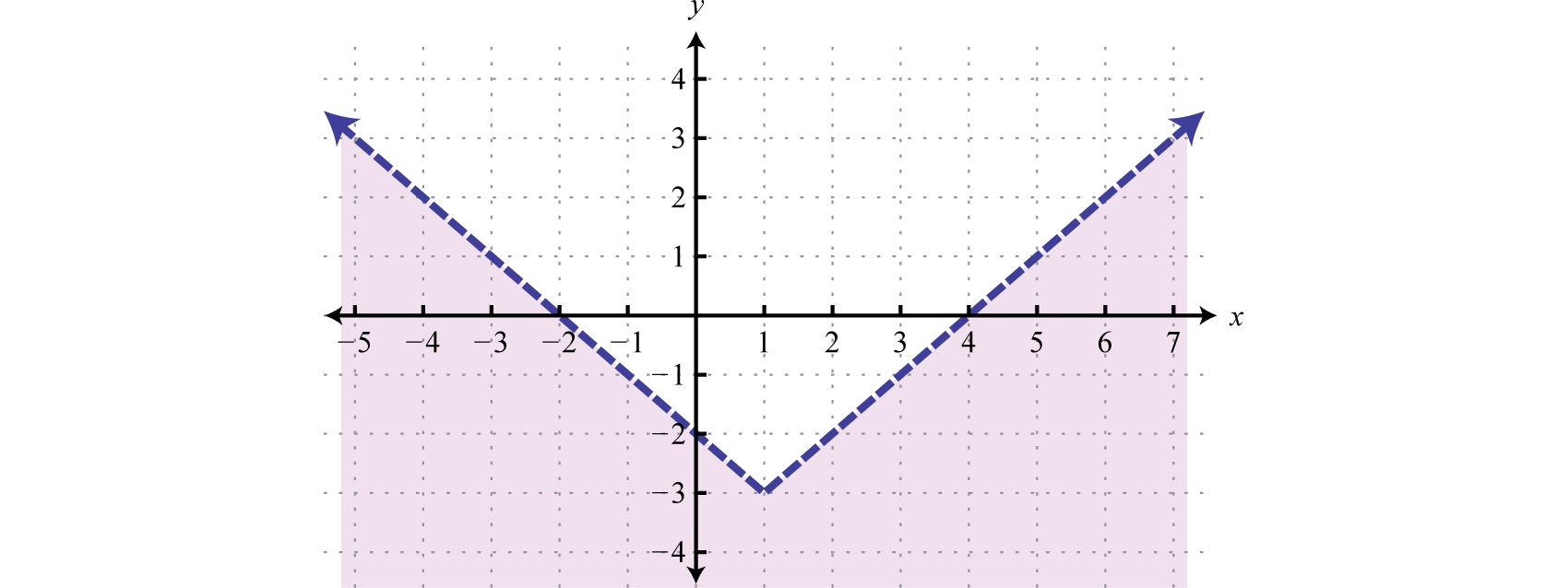
Effort this! Graph the solution set $y<\left|\mathrm{ten}-\mathrm{one}\right|-3.$

Answer:

Key Takeaways

• Linear inequalities with ii variables have infinitely many ordered pair solutions, which can be graphed by shading in the appropriate half of a rectangular coordinate plane.
• To graph the solution set of an inequality with two variables, offset graph the boundary with a dashed or solid line depending on the inequality. If given a strict inequality, employ a dashed line for the purlieus. If given an inclusive inequality, use a solid line. Side by side, cull a test point non on the purlieus. If the exam point solves the inequality, then shade the region that contains it; otherwise, shade the opposite side.
• Check your answer by testing points in and out of the shading region to verify that they solve the inequality or non.

Topic Exercises

Part A: Solutions to Inequalities with 2 Variables

Is the ordered pair a solution to the given inequality?

1. $\mathrm{five}x-y>-2\text{;}\left(-\mathrm{three},-4\right)$

2. $\mathrm{iv}x-y<-8\text{;}\left(-3,-10\right)$

3. $$6x-\mathrm{xv}y\ge -\mathrm{one}\text{;}\left(\frac{1}{2},-\frac{\mathrm{one}}{\mathrm{iii}}\right)$$

4. $$\mathrm{10}-\mathrm{two}y\ge \mathrm{two}\text{;}\left(\frac{2}{3},-\frac{5}{6}\right)$$

5. $$\frac{\mathrm{three}}{\mathrm{four}}x-\frac{2}{3}y<\frac{3}{\mathrm{two}}\text{;}\left(\mathrm{ane},-\mathrm{ane}\right)$$

6. $$\frac{\mathrm{two}}{5}\mathrm{10}+\frac{4}{3}y>\frac{\mathrm{one}}{2}\text{;}\left(-\mathrm{ii},\mathrm{one}\right)$$

7. $y\le x^{\mathrm{ii}}-1$ ; $\left(-1,1\right)$

8. $y\ge x^{\mathrm{ii}}+\mathrm{iii}$ ; $\left(-2,0\right)$

9. $y\ge {\left(\mathrm{ten}-5\right)}^2+1$ ; $\left(3,4\right)$

10. $y\le \mathrm{two}{\left(\mathrm{10}+\mathrm{one}\right)}^2-3$ ; $\left(-\mathrm{one},-2\right)$

11. $y>\mathrm{three}-\left|\mathrm{ten}\right|$ ; $\left(-4,-3\right)$

12. $y<\left|x\right|-\mathrm{eight}$ ; $\left(5,-7\right)$

13. $y>\left|\mathrm{two}x-1\right|-3$ ; $\left(-\mathrm{i},3\right)$

14. $y<\left|\mathrm{iii}x-2\right|+\mathrm{two}$ ; $\left(-\mathrm{two},10\right)$

Part B: Graphing Solutions to Inequalities with Two Variables.

Graph the solution set up.

15. $y<2x-1$

16. $y>-\mathrm{four}\mathrm{ten}+1$

17. $y\ge -\frac{\mathrm{ii}}{\mathrm{iii}}x+3$

18. $y\le \frac{4}{\mathrm{iii}}x-3$

19. $2x+3y\le 18$

20. $\mathrm{v}x+\mathrm{ii}y\le 8$

21. $6\mathrm{ten}-5y>\mathrm{thirty}$

22. $8x-\mathrm{six}y<24$

23. $3x-4y<0$

24. $x-3y>0$

25. $x+y\ge 0$

26. $x-y\ge 0$

27. $y\le -2$

28. $y>-\mathrm{iii}$

29. $\mathrm{10}<-2$

30. $x\ge -3$

31. $$\frac{1}{6}x+\frac{1}{10}y\le \frac{1}{\mathrm{two}}$$

32. $$\frac{3}{8}x+\frac{\mathrm{ane}}{2}y\ge \frac{\mathrm{iii}}{4}$$

33. $$\frac{1}{12}\mathrm{10}-\frac{1}{\mathrm{six}}y<\frac{2}{3}$$

34. $$\frac{\mathrm{ane}}{3}\mathrm{10}-\frac{1}{9}y>\frac{4}{3}$$

35. $5\mathrm{ten}\le -\mathrm{iv}y-12$

36. $-\mathrm{four}x\le 12-3y$

37. $\mathrm{iv}y+2<3\mathrm{10}$

38. $8x<9-\mathrm{half\; dozen}y$

39. $\mathrm{v}\ge \mathrm{three}\mathrm{ten}-15y$

40. $$2\mathrm{10}\ge 6-9y$$

41. Write an inequality that describes all points in the upper half-plane above the 10-axis.

42. Write an inequality that describes all points in the lower half-plane below the x-axis.

43. Write an inequality that describes all points in the one-half-plane left of the y-axis.

44. Write an inequality that describes all points in the half-plane right of the y-axis.

45. Write an inequality that describes all ordered pairs whose y-coordinate is at to the lowest degree k units.

46. Write an inequality that describes all ordered pairs whose x-coordinate is at near thou units.

Graph the solution set.

47. $y\le x^{\mathrm{ii}}+3$

48. $y>x^2-2$

49. $y\le -x^2$

50. $y\ge -x^2$

51. $y>{\left(\mathrm{ten}+1\right)}^{\mathrm{ii}}$

52. $y>{\left(x-2\right)}^2$

53. $y\le {\left(x-1\right)}^2+2$

54. $y\le {\left(x+3\right)}^2-\mathrm{ane}$

55. $y<-{\mathrm{ten}}^2+\mathrm{ane}$

56. $y>-{\left(\mathrm{10}-2\right)}^{\mathrm{ii}}+\mathrm{one}$

57. $y\ge \left|\mathrm{10}\right|-\mathrm{ii}$

58. $y<\left|x\right|+1$

59. $y<\left|\mathrm{ten}-3\right|$

60. $y\le \left|x+2\right|$

61. $y>-\left|\mathrm{ten}+\mathrm{one}\right|$

62. $y\le -\left|\mathrm{10}-2\right|$

63. $y\ge \left|\mathrm{ten}+\mathrm{three}\right|-2$

64. $y\ge \left|x-2\right|-\mathrm{ane}$

65. $y<-\left|x+4\right|+2$

66. $y>-\left|x-4\right|-\mathrm{i}$

67. $y>x^3-1$

68. $y\le {\mathrm{10}}^3+2$

69. $y\le \sqrt{x}$

70. $y>\sqrt{\mathrm{ten}}-\mathrm{i}$

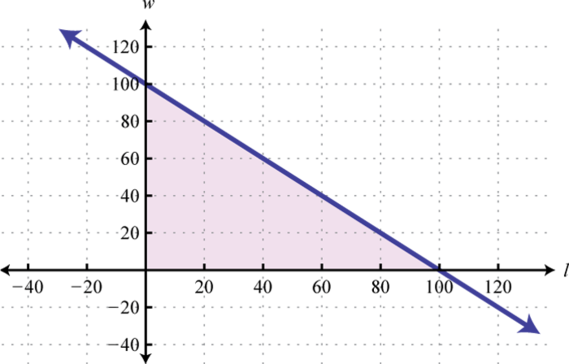
71. A rectangular pen is to be synthetic with at almost 200 feet of fencing. Write a linear inequality in terms of the length l and the width w. Sketch the graph of all possible solutions to this problem.

72. A company sells one product for $8 and some other for $12. How many of each production must be sold so that revenues are at to the lowest degree $2,400? Permit ten represent the number of products sold at $8 and let y represent the number of products sold at $12. Write a linear inequality in terms of x and y and sketch the graph of all possible solutions.

Answers

1. No

3. Yes

5. Yeah

7. No

9. No

11. No

13. Yes

15. 

17. 

19. 

21. 

23. 

25. 

27. 

29. 

31. 

33. 

35. 

37. 

39. 

41. $y>0$

43. $\mathrm{10}<0$

45. $y\ge \mathrm{grand}$

47. 

49. 

51. 

53. 

55. 

57. 

59. 

61. 

63. 

65. 

67. 

69. 

71. $l+w\le 100$ ;

    

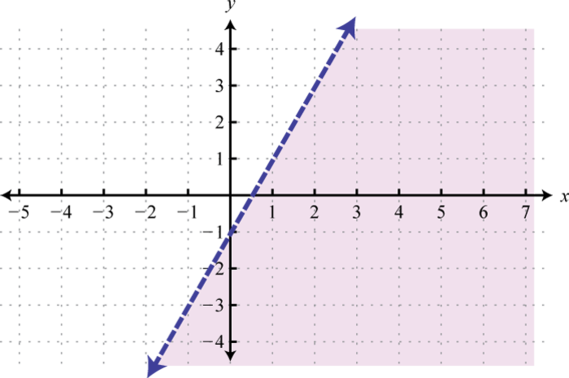
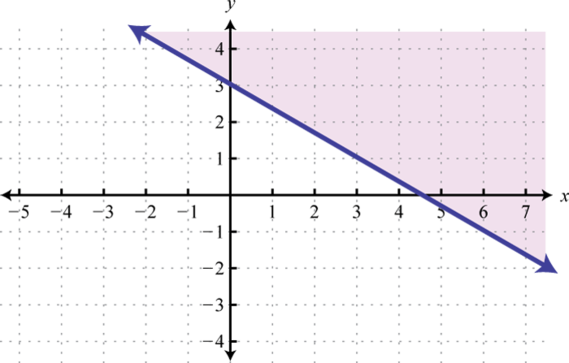
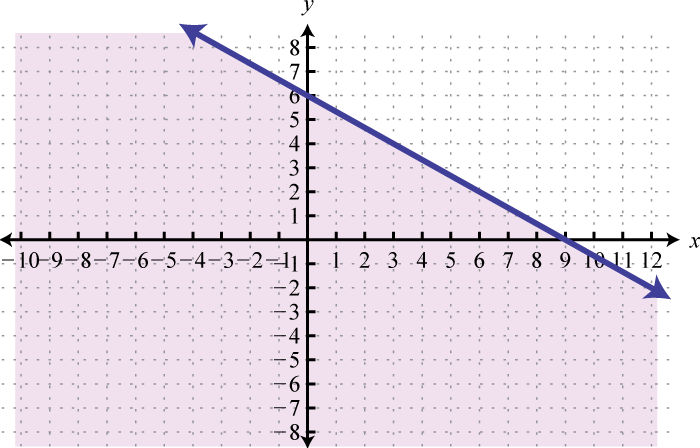
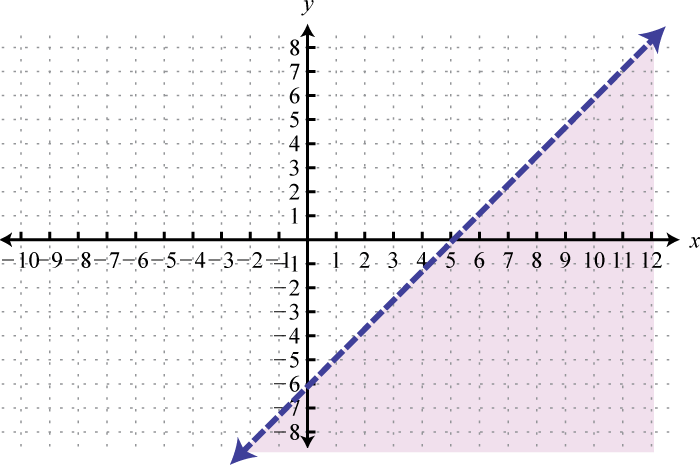
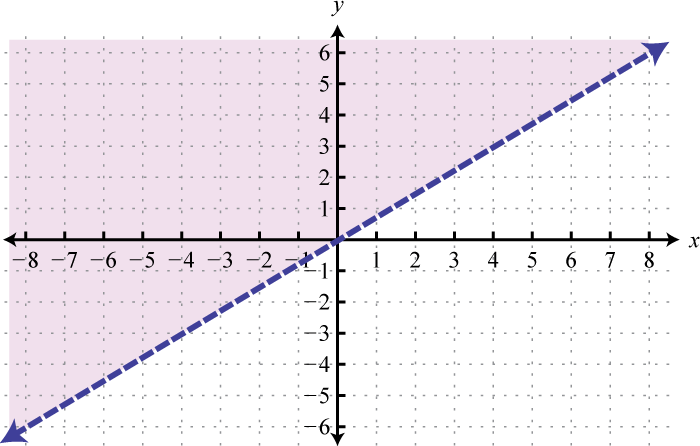
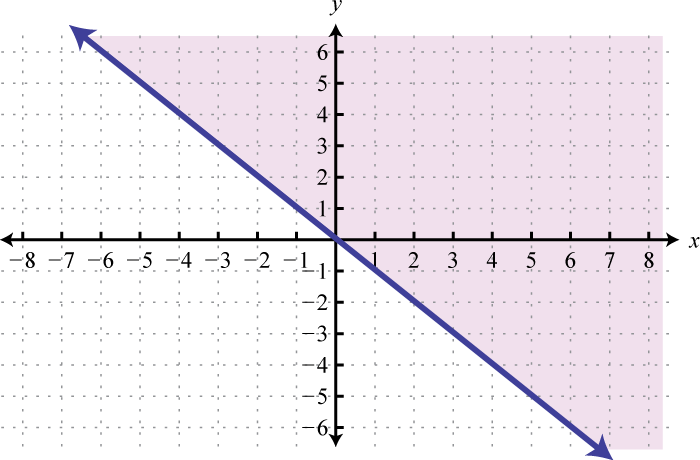
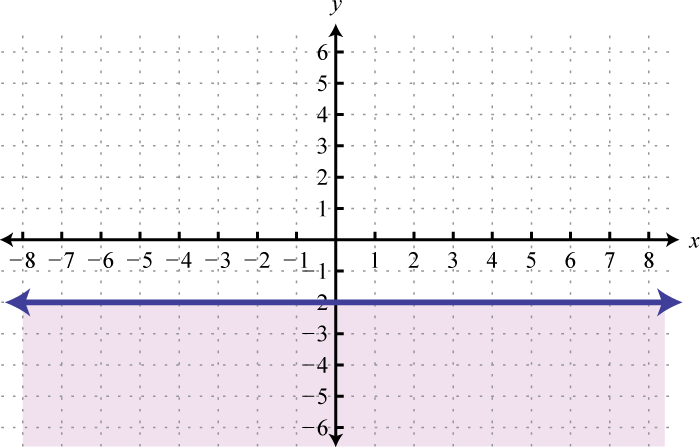
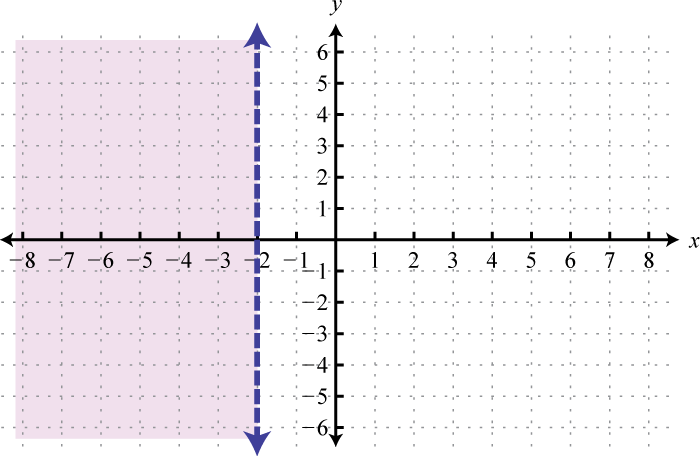
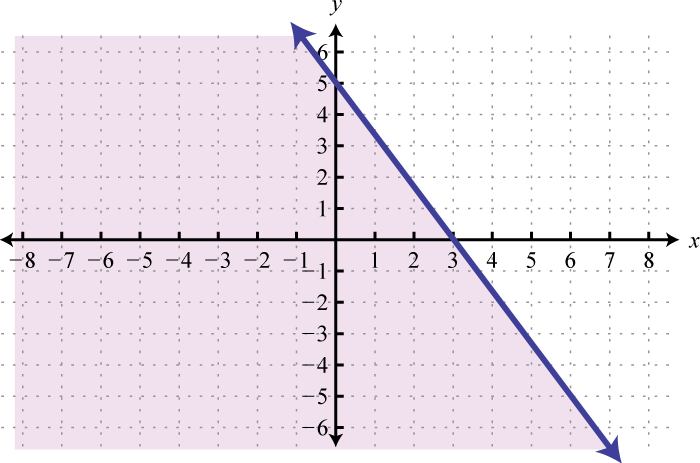
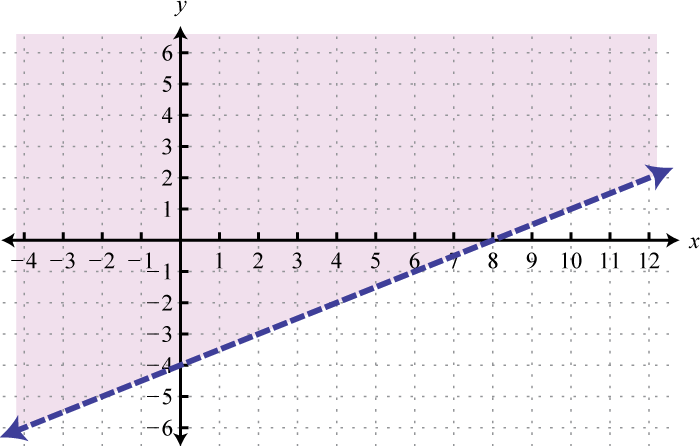
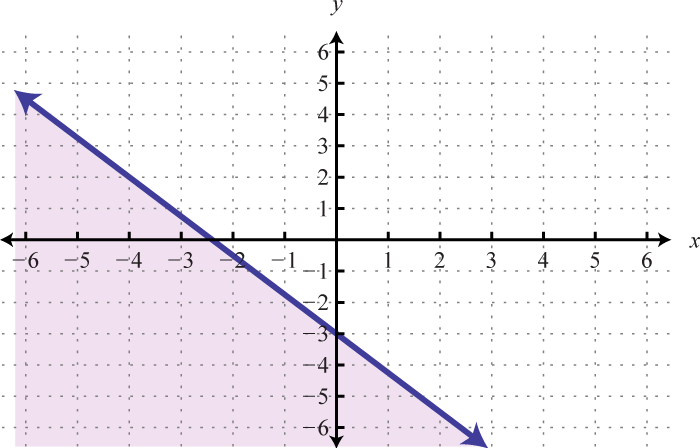
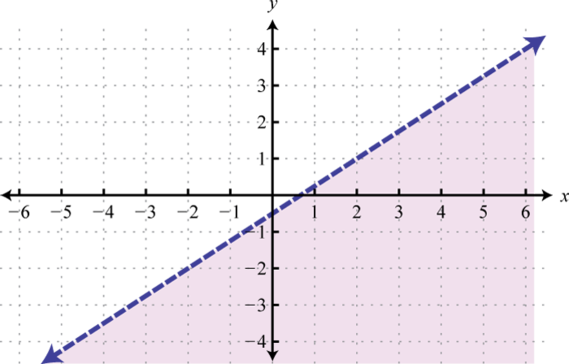
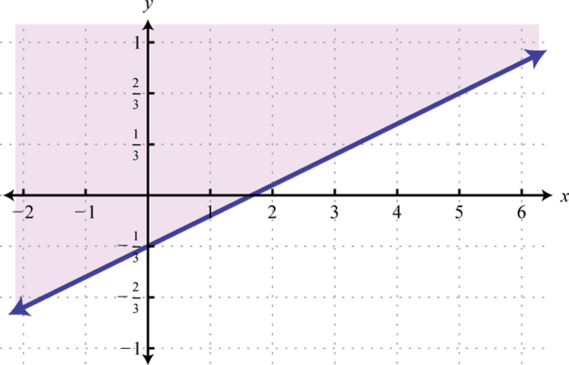
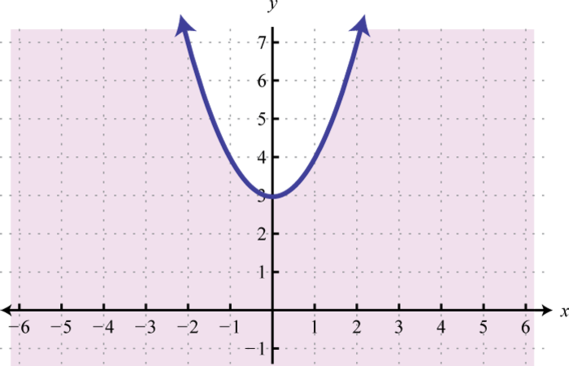
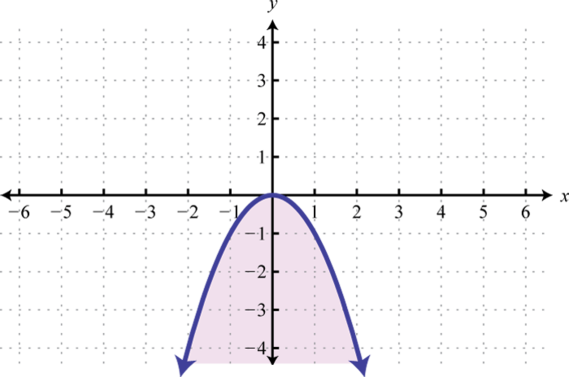
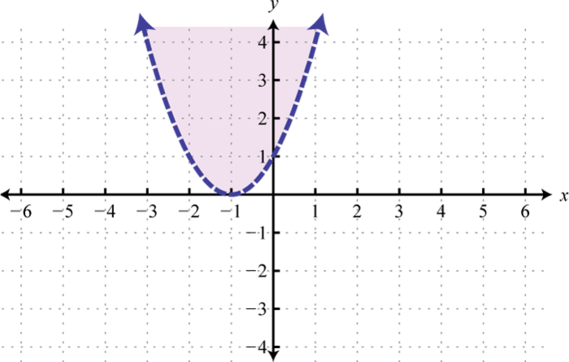
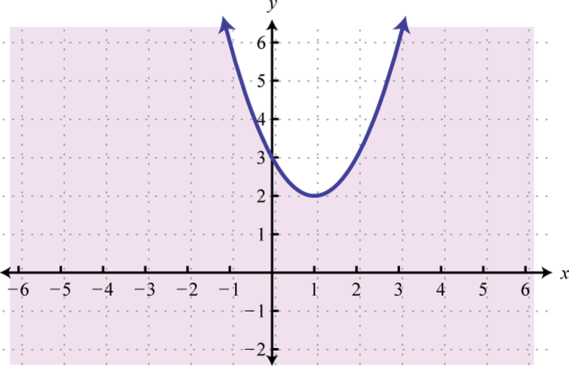
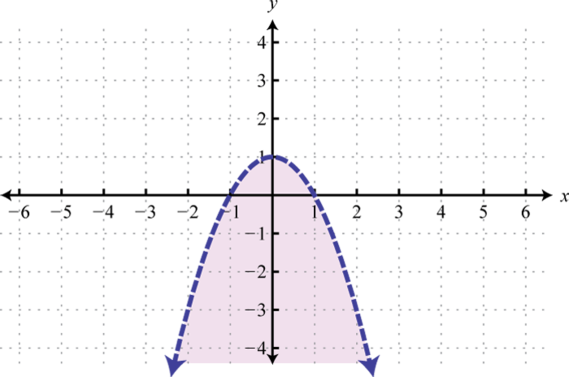
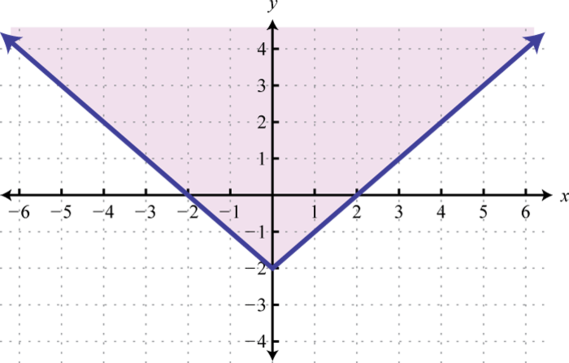
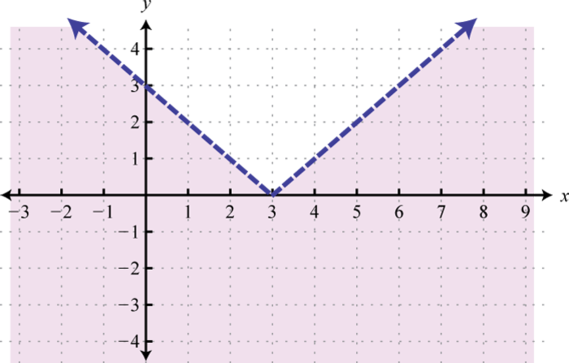
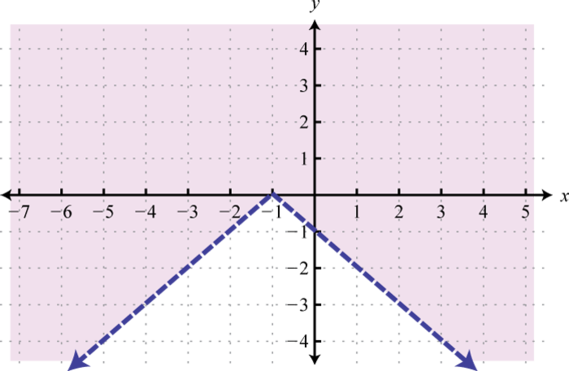
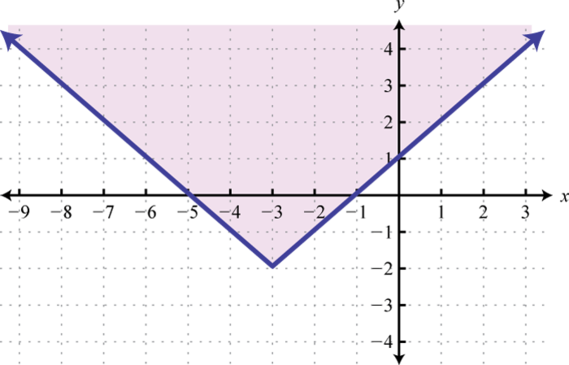
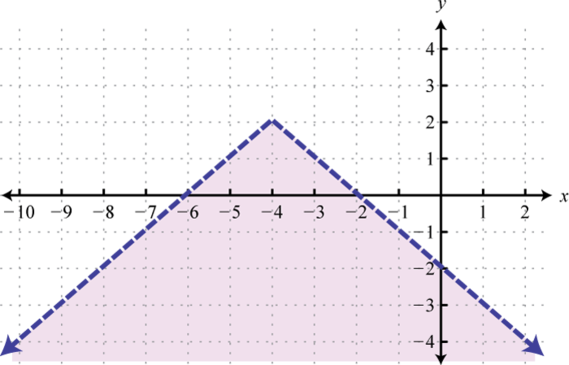
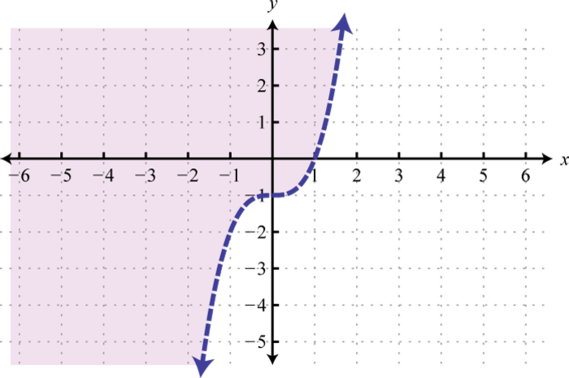
How To Graph A Solution Set Of Inequalities,

Source: https://saylordotorg.github.io/text_intermediate-algebra/s05-07-solving-inequalities-with-two-.html

Posted by: lealpolornet.blogspot.com

Share this post